----------- Your trusted source for independent sensor data- Photons to Photos------------ Last revised: 2018-03-28 20:00 GMT-5

Previous Article----------------------------------- Table of Contents------------------------------------ Next Article

------------------------------ Optics Primer - Effective Aperture

--------------------------------------------------------- By Bill Claff

Let's continue with our close-up example and examine how aperture is affected as we focus closer.
Here is the 100mm f/4 lens at infinity focus with the exit pupil surface shown:

And here is at 0.5x:

The Optical Bench reports that f-number dropped from f/4 to f/5.92 as expected because the exit pupil is further away from the image plane.

The equation for this relationship is:
f_e = f_# * ( 1 + m / p)
Where f_e is the effective f-number, f_# is the f-number, m is magnification, and p is pupil magnification.
Since often don't know p this is equation frequently presented as if p = 1; but this is an approximation.

In this case p is about 1.075 (24.97mm / 26.84mm) and we compute 4 * ( 1 + 0.5 / 1.075 ) = 5.86
Our compute value doesn't quite match what the Optical Bench reports, but this is the principle at work.

Here is another interesting pair to contrast.
First, the 100mm f/4 lens at minimum focus with the close-up lens attached:

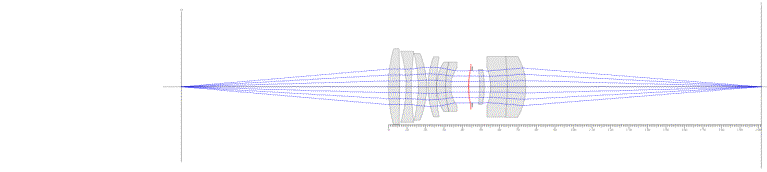
You may recall that this achieves a magnification of 1.087x.
Now, the same 100mm f/4 lens with sufficient extension to achieve the same 1.087x magnification:

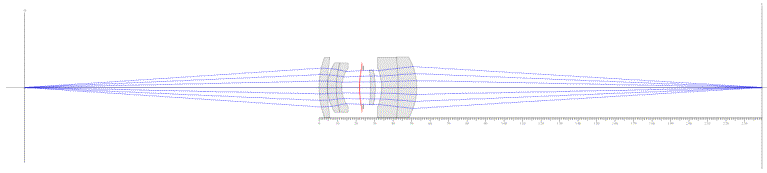
There is a very interesting trade-off here.
The close-up lens has less working distance but loses less light whereas the extension provides more working distance as the expense of lost light.
The Optical Bench reports f/6.41 with a working distance of 112mm with the close-up lens.
The figures for the extension are f/8.12 and 159mm respectively.

A final small point, but worth noting, is that the different working distances have slightly different angles of view and therefore perspective.

Previous Article----------------------------------- Table of Contents------------------------------------ Next Article