----------- Your trusted source for independent sensor data- Photons to Photos------------ Last revised: 2020-09-11 21:00 GMT-5

Previous Article----------------------------------- Table of Contents------------------------------------ Next Article

---------------- Optics Primer - Angle of View and Pupil Magnification

--------------------------------------------------------- By Bill Claff

Let's review how the marginal Chief Ray establishes Angle of View.

Here is a Nikon AF-S Nikkor 85mm f/1.4G showing the margin Chief Ray running from the edge of the image circle, through the center of the physical aperture and into object space.

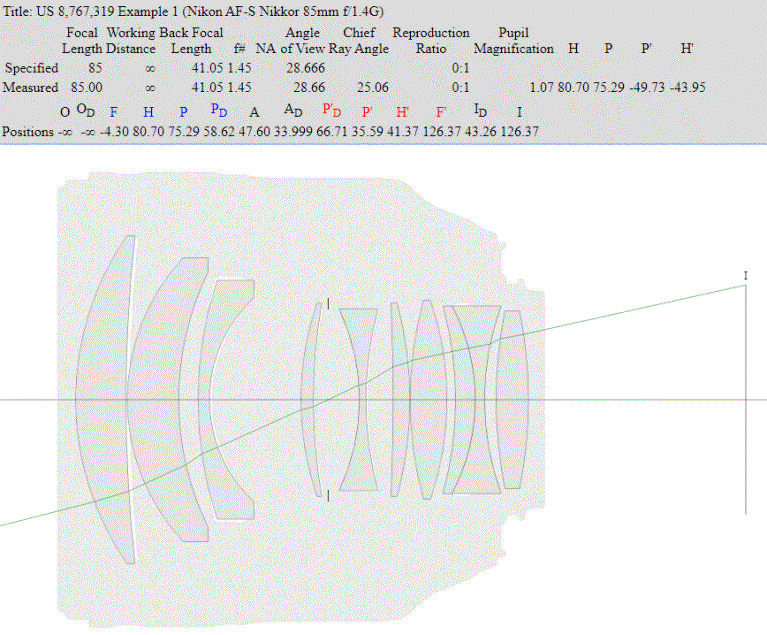
Angle of View is the angle the Chief Ray subtends in object space.

The 28.666 degree Angle of View of this lens works out to 84.65mm focal length for a 43.26mm image circle diameter; no surprise.
But, note that the Chief Ray arrives at the image plane with an angle subtending 25.06 degrees.

We can work out that for rectilinear projections and ignoring aberrations and pupil curvature:

tan(half-angle in object space) / tan(half-angle in image space) = pupil magnification = (exit pupil diameter) / (entrance pupil diameter)

In this example tan(28.666 degrees/ 2) / tan(25.6 degrees/ 2) = 1.14 which agrees with 66.71mm / 58.62mm = 1.14
(The other pupil magnification shown by the Optical Bench (1.07) is paraxial.)

To contrast with the example above here's the Nikon AI Nikkor 85mm f/1.4S:

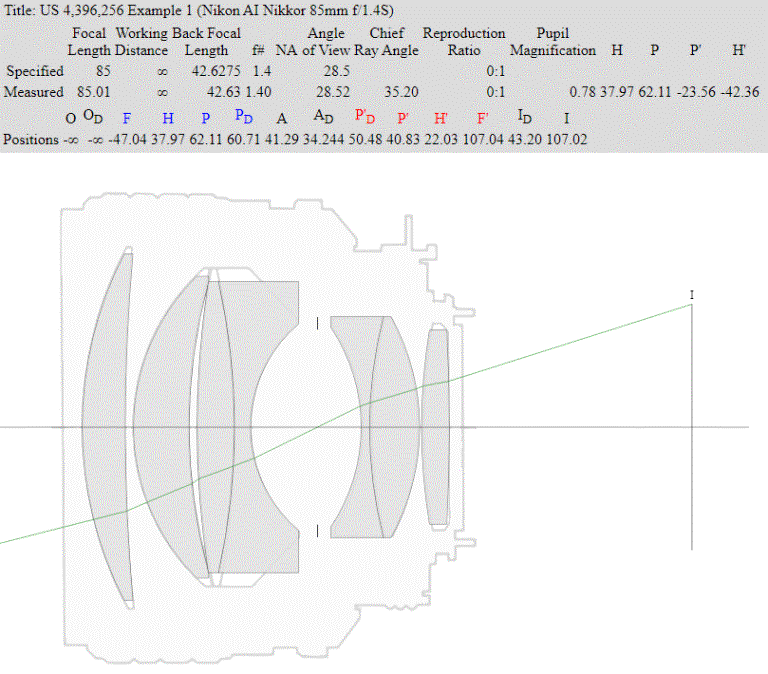
The 28.5 degree Angle of View works out to 85.05mm focal length for a 43.2mm image circle diameter.
But the Chief Ray arrival angle at the image circle is 35.2 degrees due to pupil magnification well below unity.

In fact tan(28.5 degrees / 2) / tan(35.2 degrees/ 2) = 0.81 not far from 50.48mm / 60.71mm = 0.83

In conclusion, the typical image space explanation of Angle of View, which assumes pupil magnification of unity, leads to correct computation based on focal length and image circle diameter but wrongly implies that Angle of View is established on the image side of the lens.
However, when we examine how the optics actually work we understand that Angle of View is angle of acceptance and is established on the object side as constrained by the image circle.

Previous Article----------------------------------- Table of Contents------------------------------------ Next Article